Concetto di rapporto incrementale
Consideriamo una funzione y=f(x) definita in un intervallo I
. Sia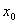 
un punto del suo dominio. Diamo a
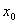un incremento h positivo, otteniamo così il punto 
. La funzione, mentre la variabile indipendente passa da
a ,
varia da 
a 
, cioè subisce l'incremento
un punto del suo dominio. Diamo a
un incremento h positivo, otteniamo così il punto
. La funzione, mentre la variabile indipendente passa d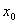a
a ,
varia da
a
, cioè subisce l'incremento
-
.
si dà il nome di rapporto incrementale della funzione
f(x) nel punto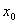
. La definizione è valida anche considerando un incremento
negativo.
Dal punto di vista geometrico, (vedi figura), il rapporto incrementale rappresenta il coefficiente angolare della retta secante passante per i punti P e Q. Ciò è facilmente comprensibile se si tiene conto che il coefficiente angolare della retta passante per P e Q è uguale a
( 
rappresenta l'angolo che la retta forma con l'asse
delle x e anche l'angolo in P ) e che:
=
.
. La definizione è valida anche considerando un incremento
negativo.Dal punto di vista geometrico, (vedi figura), il rapporto incrementale rappresenta il coefficiente angolare della retta secante passante per i punti P e Q. Ciò è facilmente comprensibile se si tiene conto che il coefficiente angolare della retta passante per P e Q è uguale a
(
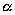rappresenta l'angolo che la retta forma con l'asse
delle x e anche l'angolo in P ) e che:
=
.(In ogni triangolo rettangolo, la tangente di un angolo
è uguale al rapporto fra la misura del cateto opposto e quella del
cateto adiacente all'angolo.)
Derivata di una funzione
Si definisce derivata prima o semplicemente derivata della funzione f(x) nel punto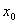
del suo dominio il limite se esiste ed è finito del rapporto
incrementale, cioè:
Si definisce derivata prima o semplicemente derivata della funzione f(x) nel punto
del suo dominio il limite se esiste ed è finito del rapporto
incrementale, cioè:
e si indica con i simboli 
, 
, 
.
,
,
.La derivata, dal punto di vista geometrico, rappresenta
il coefficiente angolare della retta tangente al grafico della funzione nel
punto P.
Infatti , tenuto conto che il rapporto incrementale è uguale al coefficiente angolare della secante e considerato che al tendere di h a 0 la secante tende a diventare la tangente, l'affermazione è senz'altro vera.
Infatti , tenuto conto che il rapporto incrementale è uguale al coefficiente angolare della secante e considerato che al tendere di h a 0 la secante tende a diventare la tangente, l'affermazione è senz'altro vera.
Calcolo di derivate di funzioni elementari
Vogliamo ora determinare le derivate di alcune funzioni
elementari. Iniziamo con f(x)=k (costante) nel punto
=1. A tal fine dobbiamo calcolare il limite
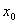=1. A tal fine dobbiamo calcolare il limiteLa derivata di una costante, indipendentemente dal punto
in cui si calcola, è uguale a 0.
Se consideriamo
nel punto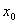
=1, avremo:
La derivata di una funzione in un punto è quindi un numero reale.
Se la derivata invece viene calcolata nel punto generico x, è a sua volta una funzione della stessa variabile.
Determiniamo adesso la derivata della funzione f(x)=x, nel punto x.
=
.
Se consideriamo
nel punto
=1, avremo:
La derivata di una funzione in un punto è quindi un numero reale.
Se la derivata invece viene calcolata nel punto generico x, è a sua volta una funzione della stessa variabile.
Determiniamo adesso la derivata della funzione f(x)=x, nel punto x.
Se
,
,
=
.A questo punto possiamo costruire una tabella con alcune
funzioni elementari e a fianco le corrispondenti derivate generiche.
La derivata è stata indicata con il simbolo y'.
La derivata è stata indicata con il simbolo y'.
