Regole di derivazione
Le principali regole di derivazione sono:
- la derivata del prodotto di una costante per una funzione;
- la derivata della somma di due o più funzioni;
- la derivata del prodotto;
- la derivata del quoziente;
- la derivata dell'inversa di una funzione.
Nel primo caso, data la funzione F(x)=kf(x),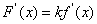 
Infatti.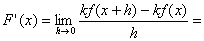
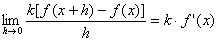
Infatti.
Si può quindi dire che la derivata del prodotto
di una costante per una funzione è uguale al prodotto della costante
per la derivata della funzione.
Se consideriamo ad esempio
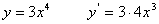, dunque 
.
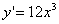La derivata della somma di due funzioni è uguale alla
somma delle derivate delle due funzioni, cioè:
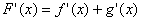
La regola ovviamente è valida anche nell'eventualita di più di due funzioni.
La dimostrazione di quanto affermato è la seguente:
, dunque
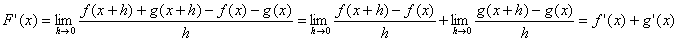
.La regola ovviamente è valida anche nell'eventualita di più di due funzioni.
La dimostrazione di quanto affermato è la seguente:
Data la funzione
F(x)=f(x)+g(x)
Cosi' se y=3x+cosx+5, y'=3-senx.
Nel caso del prodotto F(x)=f(x)g(x) si ha:
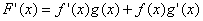
La derivata di un prodotto di due funzioni è uguale alla somma del prodotto della derivata della prima per la seconda non derivata con la prima non derivata per la derivata della seconda.
Nel caso del prodotto F(x)=f(x)g(x) si ha:
La derivata di un prodotto di due funzioni è uguale alla somma del prodotto della derivata della prima per la seconda non derivata con la prima non derivata per la derivata della seconda.
Data ad esempio la funzione
y=3xsenx , y'=3senx+3xcosx
Nel quoziente
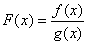
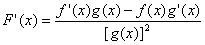
La derivata del quoziente di due funzioni è uguale
ad un rapporto che ha al numeratore la differenza fra il prodotto della
prima derivata per la seconda non derivata e il prodotto della prima non
derivata per la seconda derivata e al denominatore, la seconda funzione
al quadrato.
Esempio:
data
.
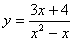
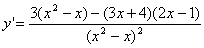Esempio:
data
.Nel caso dell'inversa di una funzione
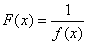
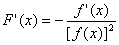
La derivata dell'inversa di una funzione è uguale
all'opposto del rapporto fra la derivata della funzione e la funzione
al quadrato.
Cosi'
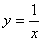
Cosi'
ha come derivata
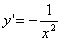
In queste righe le funzioni sono state scritte a volte
con la lettera F, a volte con la y, ciò non deve destare dubbi in quanto
tutte e due le lettere si possono utilizzare per indicarle.